Exemplos de Osciladores

Pêndulo Simples

Um pêndulo simples é um fio inextensível de comprimento $L$ e de massa desprezível fixado em uma de suas extremidades e com um corpo de massa $m$ preso à outra extremidade do fio. Quando o pêndulo é retirado de sua posição de equilíbrio, com um ângulo de abertura $\alpha$ em relação à vertical, e solto, o pêndulo começa a oscilar.

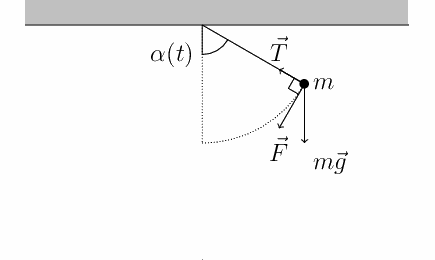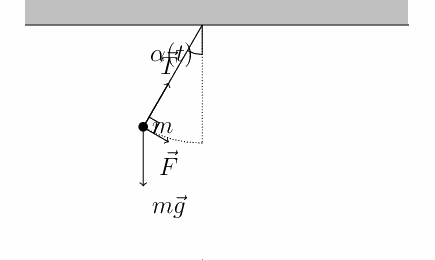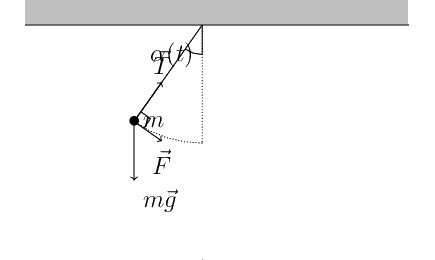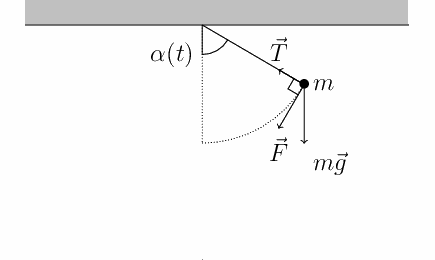
Pêndulo simples sem atrito

A amplitude do movimento será a distância entre a posição de equilíbrio e a posição extrema ocupada pelo corpo que oscila. É possível demonstrar que o período de oscilação de um pêndulo simples oscilando com pequena amplitude $( \alpha \leq 15 º)$ e sem atrito é dado pela expressão

$T = 2\pi \sqrt\frac{L}{g}$

onde $L$ é o comprimento do pêndulo simples e $g$ é a aceleração da gravidade local.
A expressão nos mostra que: quanto maior for o comprimento $L$ do pêndulo, maior será o seu período; quanto maior for a aceleração da gravidade no local onde o pêndulo oscila, menor será o seu período; o período não depende da massa $m$ do pêndulo.

Oscilador Harmônico Linear Simples

Um bloco de massa m conectado a uma mola com uma constante elástica k está inicialmente em repouso, sobre um piso horizontal sem atrito.

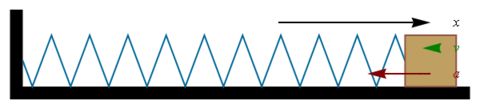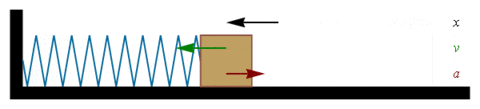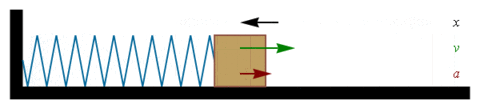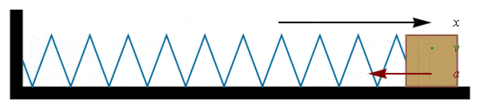
Oscilador harmônico linear sem atrito

O bloco é então deslocado de sua posição inicial esticando a mola. O bloco é então solto. Este constitui um exemplo de um oscilador harmônico linear. Neste caso é possível demonstrar, desconsiderando todas as forças de atrito, que o período de seu movimento é

$T = 2\pi \sqrt\frac{m}{k}$

onde $T$ é o período (ou seja, o tempo necessário para que o objeto realize um ciclo completo), $m$ é a massa do objeto que está oscilando e $k$ é a constante elástica da mola. Observe que neste caso, ao contrário do pêndulo, o período depende da massa do corpo que oscila: quanto maior a massa, maior será o período do pêndulo. Nos sistemas que se comportam como osciladores sempre existe uma força que tende a retornar o objeto oscilante para a sua posição de equilíbrio. Esta força é chamada de força restauradora. No caso do pêndulo, a força restauradora está associada à gravidade e, no caso do oscilador harmônico simples a força restauradora está associada às propriedades elásticas da mola.

Abaixo, temos um simulador que vai facilitar o entendimento da relação existente entre período, massa e constante da mola.