Sentido de propagação de uma onda

Como vimos na seção anterior, a equação de uma onda pode ser expressa por

$y(x,t) = Asen (kx - \omega t)$

Ou por

$y(x,t) = Asen (kx + \omega t)$

Mas qual o significado físico em se usar o sinal positivo ou negativo?
Vejamos o primeiro caso. Façamos kx – ωt igual a uma certa quantidade alfa, ou seja

$kx - \omega t = \alpha$

Isolando x nesta equação temos:

$x = \frac {\alpha}{k} + \frac {\omega t}{k}$

Notamos na equação que com o transcorrer do tempo, ou seja, quando o tempo $t$ cresce, $x$ também cresce. Isso significa que a onda está se deslocando no sentido de $x$ crescente (para a direita).

Vejamos agora o segundo caso. Façamos $kx + \omega t$ igual à quantidade $\alpha$ e teremos:

$kx = \omega t = \alpha$

Isolando $x$ nesta última expressão ficamos com:

$x = \frac {\alpha}{k} + \frac {\omega t}{k}$

Vemos agora da equação, que com o transcorrer do tempo, ou seja, quando o tempo $t$ cresce, $x$ diminui. Isto significa que a onda está se deslocando no sentido de $x$ decrescente (para à esquerda).

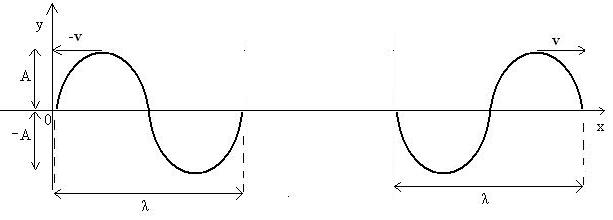
Resumindo, a equação de uma onda pode ser escrita como:

$y(x,t) = Asen(kx \pm \omega t)$

Sendo

$y(x,t) = Asen(kx - \omega t), (x crescendo)$

$y(x,t) = Asen(kx + \omega t), (x decrescendo)$