Uma onda deslocando numa corda esticada pode assumir muitas formas, mas a propriedade fundamental para cada onda é o seu comprimento de onda (lâmbda) e sua frequência . O comprimento de onda é a distância que a onda percorre durante um período , isto é, o comprimento de onda de uma onda, é a distância mais curta, na qual o padrão da onda (sendo mantido constante) repete-se completamente. A frequência é o número de oscilações transversais por unidade de tempo que qualquer elemento da corda sofre devido à passagem da onda. A frequência da onda é a frequência da fonte oscilante.

Definimos uma fonte de onda através da relação, , de um elemento da corda em função da posição e do tempo , daquele elemento ao longo da corda. Para um estudo específico, iremos escolher a onda  abaixo, gerada pelo movimento de uma das extremidades da corda, transversalmente, em movimento periódico.

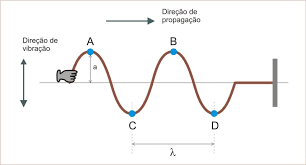
Escrevemos para a relação entre o deslocamento transversal de qualquer elemento da corda na posição e no tempo .

   

onde e são constantes e A é a amplitude da onda, sendo a amplitude o deslocamento máximo de . Em alguns textos a amplitude A é representada por onde o subscrito indica máximo. A quantidade é conhecida como fase da onda. Podemos escrever também para a equação do deslocamento a forma . Outra forma aceitável para o deslocamento é .

Todas as formas de onda, podem ser construídas pela soma das ondas senoidais, cujos comprimentos de onda e amplitudes de onda devem ser cuidadosamente selecionadas para se obter a forma de onda desejada. Dessa forma, o entendimento das ondas senoidais é a chave para o entendimento de ondas de qualquer forma.

As variáveis e entendem-se de -∞ a +∞, ou seja, elas não possuem limites. Isto quer dizer que a equação descreve uma onda numa corda de comprimento infinito, existindo para todo o tempo, desde um passado distante a um futuro longínquo distante. Na prática, são consideradas apenas variações razoavelmente pequenas de cada variável.