Fenômenos ondulatórios

Princípio de Superposição

Pode acontecer que duas ou mais ondas passem numa mesma região do espaço ao mesmo tempo. Seja, por exemplo, duas ondas 1 e 2 se deslocando simultaneamente ao longo de uma mesma corda esticada. O deslocamento da corda quando ambas as ondas atuam será:

$y(x,t) = y_1(x,t) + y_2 (x,t)$

Onde $y_1(x,t)$ e $y_2 (x,t)$ são os dois deslocamentos que a corda experimentaria se cada onda agisse separadamente. Esse é um exemplo do princípio de superposição, largamente utilizado na física, que se observa com bastante frequência em acústica.

As Figuras abaixo mostram dois pulsos, gerados nas extremidades de uma corda.

a) Interferência construtiva b) Interferência destrutiva

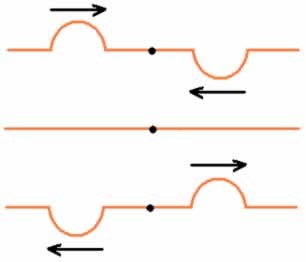
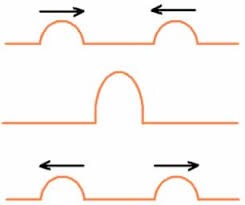
No ponto onde as duas ondas se encontraram (no mesmo tempo e espaço) dizemos que ouve uma interferência. O fenômeno de interferência acontece com todos os tipos de ondas e é exclusivo do movimento ondulatório. Abaixo temos um link para o vídeo dos dois tipos de interferência.

Link: https://www.youtube.com/watch?v=y8twOGd3NUQ

Interferência de Ondas

Interferência é o fenômeno de cancelamento ou de reforço quando uma ou mais ondas se superpõem. Seja, por exemplo, duas ondas que caminham ao longo de uma mesma corda esticada com a mesma frequência angular $\omega$ e o mesmo número de onda angular $k$ , definidas por

$y_1 (x,t) = A_1 sen (K x - \omega t + \phi )$

$y_2 (x,t) = A_2 sen (K x - \omega t)$

Onde $A_1$ e $A_2$ são as amplitudes das ondas $y_1 (x,t)$ e $y_2 (x,t)$ , respectivamente. Estas duas ondas caminham no mesmo sentido ( $x$ crescente) com a sua velocidade sendo dada pela expressão [/latex]v = \frac {\omega}{k}[/latex]. As ondas $y_1 (x,t)$ e $y_2 (x,t)$ diferem apenas por uma constante $\phi$ , a qual é chamada de diferença de fase, que representa a diferença de fase entre as duas ondas.
Aplicando o Princípio da Superposição, a onda resultante $y (x,t)$ , da combinação destas duas ondas será

$y (x,t) = y_1 (x,t) + y_2 (x,t)$

$y (x,t) = A_1 sen (K x - \omega t + \phi) + A_2 sen (k x - \omega t)$

Por questão de simplicidade trataremos apenas do caso em que as amplitudes das duas ondas sejam iguais, ou seja, $A_1 = A_2 = A$ . Fazendo-se isto na questão anterior e definindo $\alpha = k x - \omega t$ , temos

$y (x,t) = A [sen (\alpha + \phi) + sen (\alpha)]$

Utilizando a relação trigonométrica: $sen (a)+ sen(b) = 2 sen [\frac {(a + b)}{2}] cos [\frac {(a - b)}{2}]$ , com $a = \alpha$ + \phi[/latex] e $b = \alpha$ , obtemos:

$y (x,t) = 2 A cos (\frac {\phi}{2}) sen (\alpha + \frac {\phi}{2})$

Lembrando que $\alpha = k x - \omega t$ , temos finalmente

$y (x,t) = 2 A cos (\frac {\phi}{2}) sen (k x - \omega t + \frac {\phi}{2})$

Notamos pela equação acima que a onda resultante também possui uma forma senoidal, diferindo das ondas originais $y_1 (x,t)$ e $y_2 (x,t)$ , somente em dois aspectos: i) pela diferença de fase $\frac {\phi}{2}$ e ii) pela amplitude, que será

$A^{*} = 2 A cos (\frac {\phi}{2})$

Dizemos, em geral, que se a onda resultante possui uma amplitude $maior$ que as amplitudes das ondas originais, a interferência é construtiva, e se a onda resultante possui uma amplitude $menor$ que as amplitudes das ondas originais, a interferência é destrutiva. Verificamos agora dois casos bem especiais:

Primeiro caso: se fizermos $\phi = 0$ , na equação $y (x,t) = 2 A cos (\frac {\phi}{2}) sen (k x - \omega t + \frac {\phi}{2})$ , ela se reduz a

$y (x,t) = 2 A cos (k x - \omega t)$

Segundo caso: Verificamos que se $\phi = \pi rad$ na equação $y (x,t) = 2 A cos (\frac {\phi}{2}) sen (k x - \omega t + \frac {\phi}{2})$ , $cos (\frac{\phi}{2} = 0$ e a onda resultante será nula:

$y (x,t) = 0$

No primeiro caso ( $y (x,t) = 2 A cos (k x - \omega t$ ), as duas ondas ( $y_1 (x,t)$ e $y_2 (x,t)$ ) estão exatamente em fase e sua interferência é dita completamente construtiva.

Notamos pela equação $A^{*} = 2 A cos (\frac {\phi}{2}$ que para $\phi = 0$ , a onda resultante possui uma amplitude que é o dobro da amplitude das ondas originais, ou seja, $A^{*} = 2 A$ , sendo este o maior valor possível para a amplitude da onda resultante.

No segundo caso, dizemos que houve uma interferência totalmente destrutiva e a amplitude da onda resultante possui seu valor mínimo, ou seja, $A^{*} = 0$ para $\phi = \pi$ na equação $A^{*} = 2 A cos (\frac {\phi}{2})$ . Para que isto ocorra, as ondas originais devem estar exatamente em oposição de fase.

Passagem de uma Onda de um Meio para Outro

Na figura abaixo, no item “a”, mostramos uma corda esticada, constituída de uma parte mais fina ligada a outra parte mais grossa. Temos então, dois meios diferentes, (1) e (2), sendo, particularmente, a densidade linear do meio (1) menor que a do meio (2), ou seja, $\mu_1 < \mu_2$ . Como tensão ( $\tau$ ) nas duas cordas é a mesma, podemos afirmar de acordo com a equação $v = \sqrt \frac{\tau}{\mu}$ , que a velocidade de propagação de uma onda na parte mais fina é maior que na parte mais grossa, ou seja, $v_1 > v_2$ .

Fazendo oscilar a extremidade da corda fina, uma onda se propaga ao longo dela e, ao atingir a corda grossa, passa a se propagar também nesta corda, isto é, a onda é transmitida da corda fina para a corda grossa (item “b” da figura). A onda que é transmitida para o meio (2) recebe o nome de onda refratada.

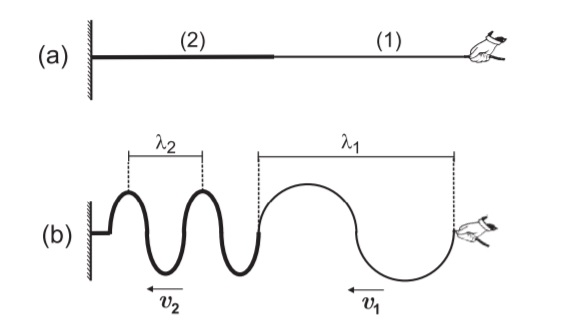
A frequência de uma onda não se altera quando ela é transmitida de um meio para o outro, sendo o valor de $f$ o mesmo para os meios (1) e (2). Pela equação $\lambda = \frac {v}{f}$ , vemos que, no meio em que a onda se propaga com maior velocidade, ela terá $maior$ comprimento de onda e no meio em que a onda se propaga com menor velocidade, ela terá um $menor$ comprimento de onda. Assim, observe que no item “b” da figura temos $\lambda_1 > \lambda_2$ , pois $v_1 > v_2$ .

Concluindo, chamamos de refração de uma onda quando uma onda passa de um meio para outro, com variação da sua velocidade de propagação e de seu comprimento de onda. Na Figura acima distinguimos então onda incidente (onda no meio 1) e a onda refratada (onda no meio 2). A onda refratada mantém a mesma frequência da onda incidente.

Links para melhor entendimento: https://www.youtube.com/watch?v=F_AYTZpJypo

https://www.youtube.com/watch?v=OWmvevbYsYg

Reflexão de uma Onda

A reflexão de uma onda ocorre quando uma onda incide sobre um obstáculo e retorna ao meio original de propagação. A onda refletida mantém a mesma velocidade e o mesmo comprimento de onda da onda incidente.
No item “a” da figura abaixo, mostramos a reflexão sofrida por um pulso quando incide em uma extremidade fixa. São mostrados quatro intervalos consecutivos de tempo $t = t_1 = t_2 = t_3, t = t_4$ . Entendemos por extremidade fixa aquela que não pode se mover. O pulso é criado por uma pessoa na extremidade direita da corda e se propaga para a esquerda. Quando o pulso chega à extremidade esquerda encontra-se com uma parede onde a corda está fixada. O pulso exerce então, uma força para cima sobre a parede. Pela lei de ação e reação (3° lei de Newton), a parede exercerá sobre a corda, uma força de mesmo módulo, mas de sentido contrário. Esta força de reação faz com que o pulso volte invertido em relação ao pulso incidente.

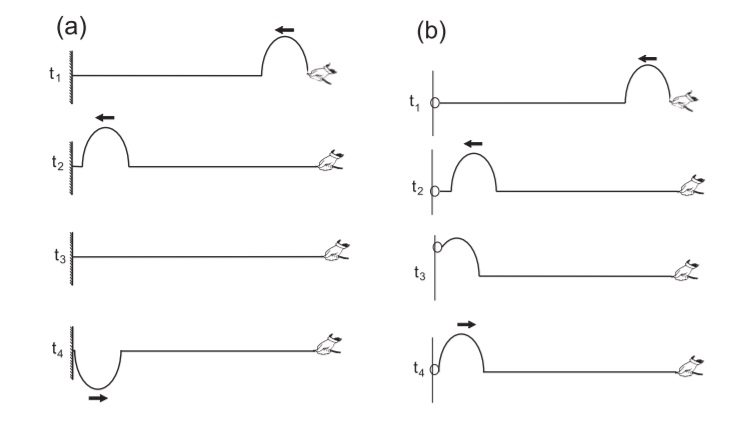
Chamamos este tipo de reflexão de reflexão rígida. Deve-se notar que o ponto onde a corda está fixada na parede não sofre um deslocamento transversal. Chamamos este ponto de nó.

No item “b” da figura acima, mostramos a reflexão sofrida por um pulso quando incide em uma extremidade livre. Uma extremidade é dita livre quando ela pode se locomover. Para isto, na extremidade esquerda da corda foi colocado um anel que pode se deslocar por uma haste. Neste caso, quando o pulso chega na extremidade esquerda da corda, o anel desliza para cima na haste puxando a corda, produzindo um pulso refletido de mesmo sinal que o pulso incidente. Este tipo de reflexão é denominado de reflexão não rígida.

Além da refração e da reflexão, existe um outro comportamento que a onda pode sofrer ao incidir sobre uma barreira: a difração. A difração de uma onda ocorre quando uma onda consegue “contornar” um obstáculo.