Movimento Ondulatório

Onda

Podemos definir uma onda como sendo uma perturbação que se propaga, carregando consigo momento, energia e informação. Toda onda possui uma certa variável física que oscila, sendo esta oscilação transmitida sucessivamente. As propriedades do movimento ondulatório são muito importantes para o entendimento do funcionamento do aparelho auditivo e da produção da fala.

Nas próximas imagens, temos alguns exemplos de ondas:

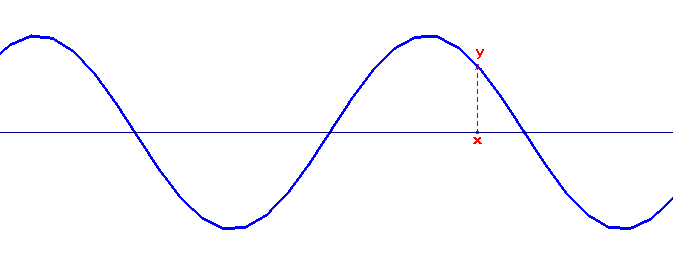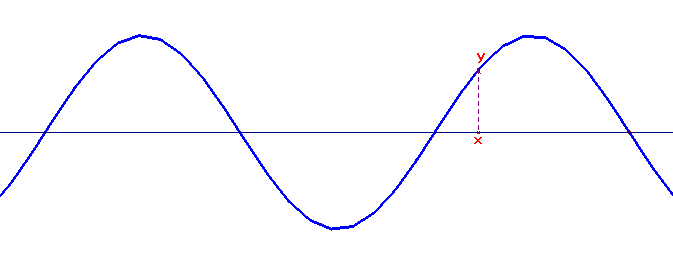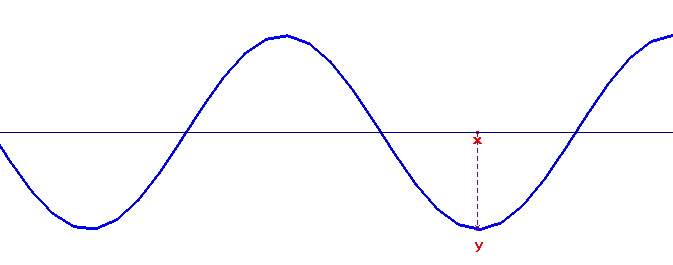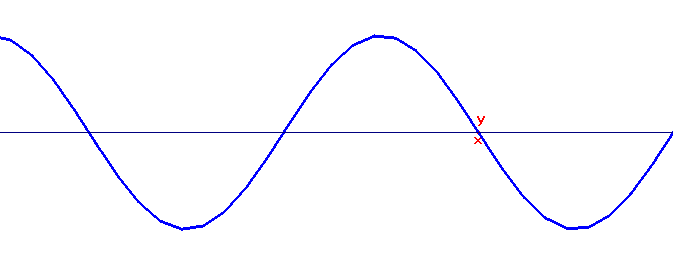
Ondas em Corda

Para um entendimento preliminar sobre ondas, tomaremos como exemplo ilustrativo nesta seção, as ondas geradas em uma corda elástica.

Ao efetuarmos um movimento brusco numa das extremidades de uma corda mantida reta, esta é percorrida por um pulso. Sendo a corda homogênea e flexível, o pulso mantém praticamente a mesma forma, à medida que se propaga. Verifica-se que a velocidade de propagação do pulso não depende da sua forma nem de como ele foi originado, depende apenas da intensidade da força e da densidade linear da corda.

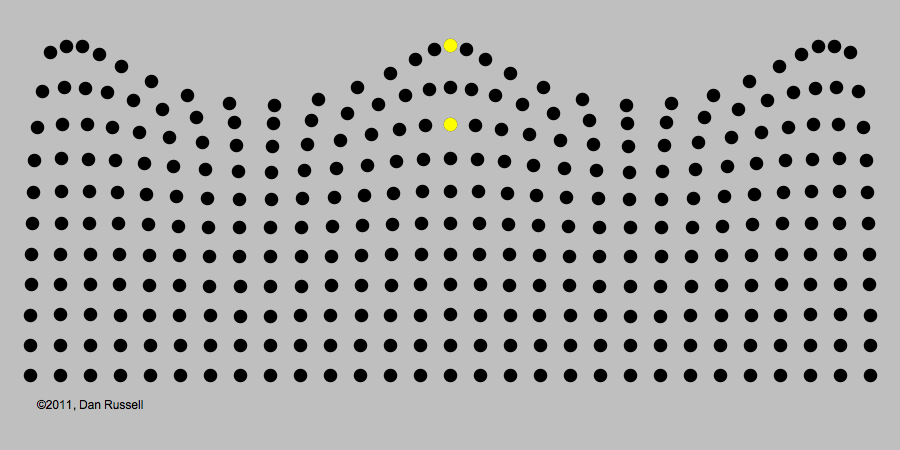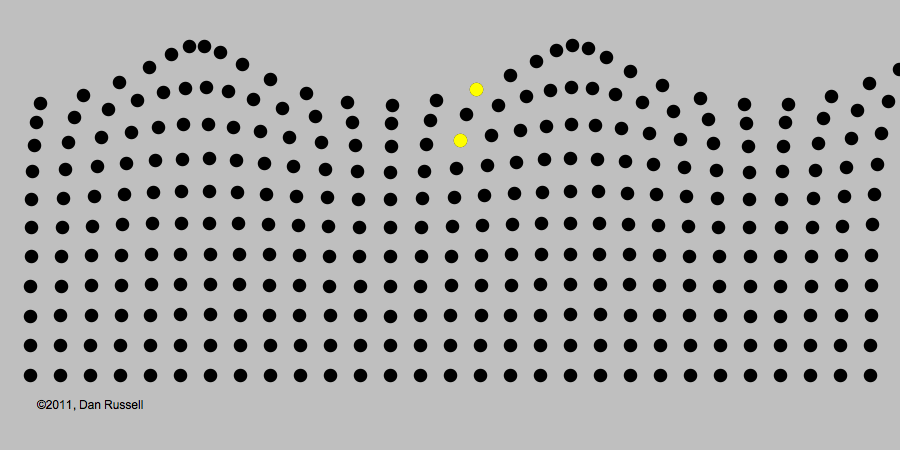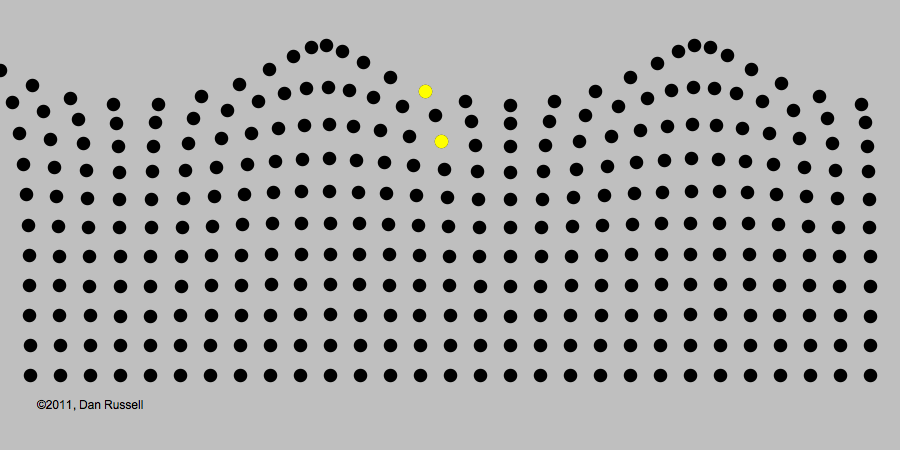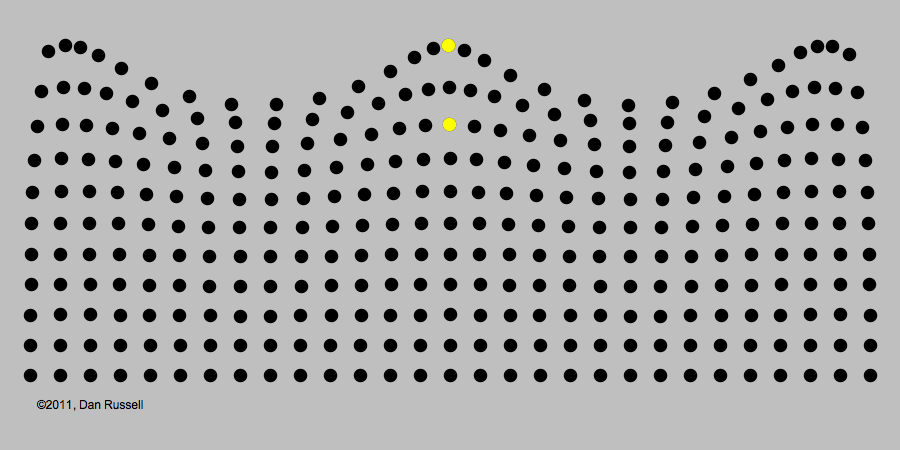
Se fixarmos nossa atenção para um determinado ponto da corda , verificaremos que este ponto se desloca para cima e para baixo, enquanto o pulso passa por ele. Devemos salientar que é apenas a perturbação (ou pulso) que se desloca ao longo da corda, enquanto seus pontos simplesmente sobem e descem à medida que o pulso passa por ela. Imaginemos, agora, que a pessoa, ao segurar a corda, movimentasse sua mão continuamente para cima e para baixo da posição inicial, com uma certa frequência constante. Neste caso, teremos uma série de pulsos (ou trem de ondas) propagando-se ao longo da corda. Dizemos que esta série de pulsos, constitui uma onda propagando-se na corda. Os pontos mais altos dos pulsos são denominados cristas da onda e os pontos mais baixos são denominados vales da onda.

Numa onda, a informação e a energia se deslocam de um ponto para outro, sem que qualquer objeto material se propague junto com a onda.

Vamos demostrar as observações relacionadas acima realizando experimentos com o simulador abaixo.

Classificação das Ondas

As ondas podem ser classificadas de diferentes modos de acordo com suas propriedades. Dentre estas classificações estão as seguintes:
a) Quanto à Natureza
Ondas mecânicas – Os dois aspectos centrais dessas ondas é que elas são governadas pelas Leis de Newton e precisam de um meio material deformável ou elástico para se propagarem. Este meio material pode ser, por exemplo, o ar, a água, uma corda esticada, uma barra de aço, etc. A perturbação é transmitida sucessivamente de um ponto a outro. As partículas do meio vibram próximas a seu ponto de equilíbrio sem se deslocar como um todo. Como as ondas mecânicas necessitam de um meio material para se propagarem, elas não se propagam no vácuo. São exemplos de ondas mecânicas o som, ondas numa mola ou corda, ondas na água, etc.

Ondas eletromagnéticas – São ondas que não necessitam de um meio material para se propagarem, podendo viajar livremente através do espaço vazio. A mais conhecida onda eletromagnética é a luz. Os raios X e as microondas também são exemplos de ondas eletromagnéticas. Todas as ondas eletromagnéticas viajam através do vácuo com a mesma velocidade c, dada por: $c \backsimeq 3 . 10^8m/s$ . Nas ondas eletromagnéticas as variáveis físicas que oscilam são os campos elétricos e magnéticos.

Ondas materiais – Sob certas condições, partículas subatômicas podem apresentar propriedades semelhantes às das ondas. Estas ondas são governadas pelas leis da Física Quântica.

b) Quanto à Dimensão
Ondas unidimensionais – Quando se propagam em uma só direção ou segundo a direção de um único eixo. Ex.: Onda numa corda, onda numa mola.

Ondas bidimensionais – Quando se propagam em duas dimensões ou em um plano formado por dois eixos. Ex.: Quando se solta uma pedra em uma bacia com água, formam-se ondas circulares em sua superfície.

Ondas tridimensionais – Quando se propagam em todas as direções, isto é, no espaço. Ex.: onda sonora.

c) Quanto a Direção de Propagação e Vibração

Onda transversal – Em uma onda transversal, os pontos do meio no qual a onda se propaga, vibram perpendicularmente à direção de propagação da onda.

Onda longitudinal – Em uma onda longitudinal, os pontos do meio no qual a onda se propaga vibram paralelamente à direção de propagação da onda.

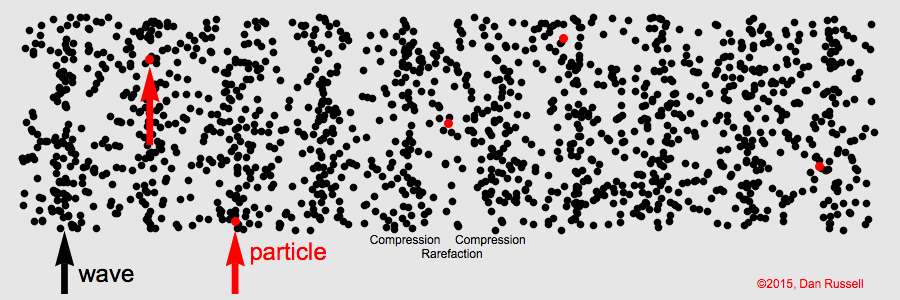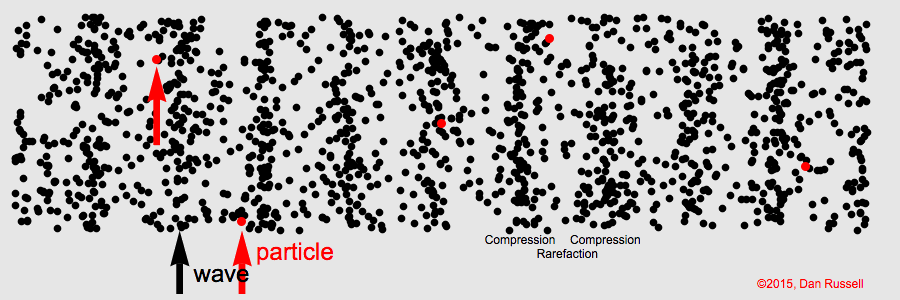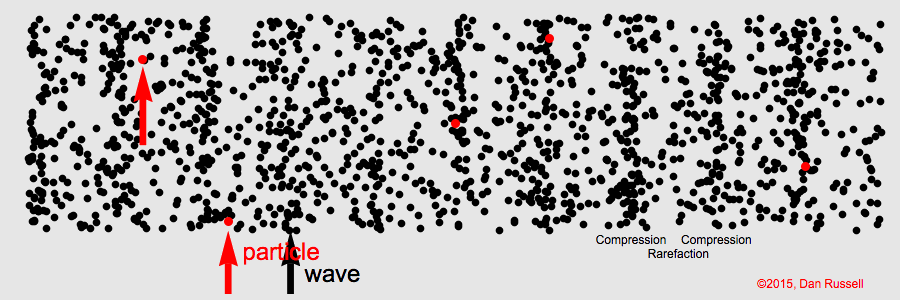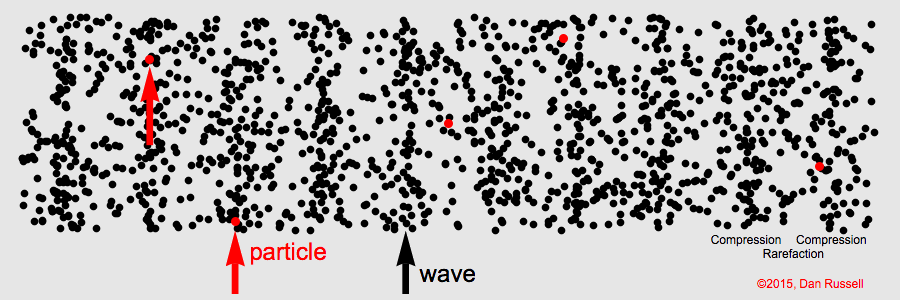
Existem, no entanto, algumas ondas que não são nem exclusivamente longitudinais e nem exclusivamente transversais. Estas ondas são conhecidas como ondas mistas.

Equação de uma Onda Progressiva

Uma onda deslocando numa corda esticada pode assumir muitas formas, mas a propriedade fundamental para cada onda é o seu comprimento de onda $\lambda$ (lâmbda) e sua frequência $f$ . O comprimento de onda é a distância que a onda percorre durante um período $T$ , isto é, o comprimento de onda de uma onda, é a distância mais curta, na qual o padrão da onda (sendo $t$ mantido constante) repete-se completamente. A frequência é o número de oscilações transversais por unidade de tempo que qualquer elemento da corda sofre devido à passagem da onda. A frequência da onda é a frequência da fonte oscilante.

Definimos uma fonte de onda através da relação, $y = f(x,t)$ , de um elemento da corda em função da posição $x$ e do tempo $t$ , daquele elemento ao longo da corda. Para um estudo específico, iremos escolher a onda abaixo, gerada pelo movimento de uma das extremidades da corda, transversalmente, em movimento periódico.

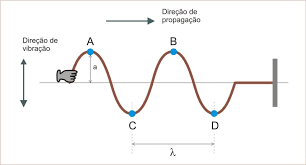
Escrevemos para a relação entre o deslocamento transversal $y$ de qualquer elemento da corda na posição $x$ e no tempo $t$ .

$y(x,t) = Asen(kx - \omega t)$

onde $k$ e $ω$ são constantes e A é a amplitude da onda, sendo a amplitude o deslocamento máximo de $y$ . Em alguns textos a amplitude A é representada por $y_m$ onde o subscrito $m$ indica máximo. A quantidade $(kx - \omega t)$ é conhecida como fase da onda. Podemos escrever também para a equação do deslocamento a forma $y(x,t) = Asen(kx + \omega t)$ . Outra forma aceitável para o deslocamento $y$ é $y(x,t) = A cos (kx - \omega t)$ .

Todas as formas de onda, podem ser construídas pela soma das ondas senoidais, cujos comprimentos de onda e amplitudes de onda devem ser cuidadosamente selecionadas para se obter a forma de onda desejada. Dessa forma, o entendimento das ondas senoidais é a chave para o entendimento de ondas de qualquer forma.

As variáveis $x$ e $t$ entendem-se de -∞ a +∞, ou seja, elas não possuem limites. Isto quer dizer que a equação descreve uma onda numa corda de comprimento infinito, existindo para todo o tempo, desde um passado distante a um futuro longínquo distante. Na prática, são consideradas apenas variações razoavelmente pequenas de cada variável.

Sentido de propagação de uma onda

Como vimos na seção anterior, a equação de uma onda pode ser expressa por

$y(x,t) = Asen (kx - \omega t)$

Ou por

$y(x,t) = Asen (kx + \omega t)$

Mas qual o significado físico em se usar o sinal positivo ou negativo?
Vejamos o primeiro caso. Façamos kx – ωt igual a uma certa quantidade alfa, ou seja

$kx - \omega t = \alpha$

Isolando x nesta equação temos:

$x = \frac {\alpha}{k} + \frac {\omega t}{k}$

Notamos na equação que com o transcorrer do tempo, ou seja, quando o tempo $t$ cresce, $x$ também cresce. Isso significa que a onda está se deslocando no sentido de $x$ crescente (para a direita).

Vejamos agora o segundo caso. Façamos $kx + \omega t$ igual à quantidade $\alpha$ e teremos:

$kx = \omega t = \alpha$

Isolando $x$ nesta última expressão ficamos com:

$x = \frac {\alpha}{k} + \frac {\omega t}{k}$

Vemos agora da equação, que com o transcorrer do tempo, ou seja, quando o tempo $t$ cresce, $x$ diminui. Isto significa que a onda está se deslocando no sentido de $x$ decrescente (para à esquerda).

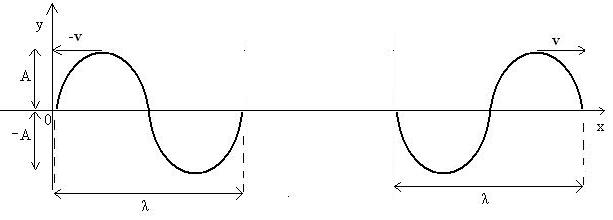
Resumindo, a equação de uma onda pode ser escrita como:

$y(x,t) = Asen(kx \pm \omega t)$

Sendo

$y(x,t) = Asen(kx - \omega t), (x crescendo)$

$y(x,t) = Asen(kx + \omega t), (x decrescendo)$

Número de Onda e Frequência Angular

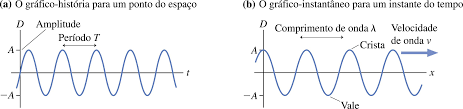
Na figura abaixo, mostramos como o deslocamento transversal $y(x,t)$ da equação $y(x,t) = Asen(kx \pm\omega t)$ varia em relação à posição $x$ num tempo determinado, escolhido com $t=0$ , isto é, a figura é um “instantâneo” da onda naquele momento. Com esta restrição, a equação acima torna-se

$y(x,0) = Asen(kx)$

Que por simplicidade escrevemos como

$y(x) = Asen(kx)$

Para um típico intervalo de comprimento de onda $\lambda = x_2 - x_1$ , podemos escrever a igualdade

$Asen(kx_1) = Asen(kx_2)$

Simplificando a constante A que aparece nos dois lados da igualdade:

$sen(kx_1) = sen(kx_2)$

Como $\lambda = x_2 - x_1$ , podemos escrever que $x_2 = \lambda + x_1$ e a equação anterior fica

$sen(kx_1) = sen(kx_1 + k \lambda)$

A função seno se repete primeiramente quando o ângulo é acrescido de $2\pi$ radianos, de forma que a equação acima será verdadeira se $k\lambda = 2\pi$ ou

$k = \frac{2\pi}{\lambda}$

Sendo $k$ conhecido como número de onda angular da onda. A relação apresentada na equação da sentido físico à quantidade $k$ que aparece na equação $y(x,t) = Asen(kx \pm \omega t)$ . A unidade de $k$ no SI é radiano por metro (rad/m).
Passamos agora nossa análise para o gráfico que mostra como o deslocamento $y$ da equação acima varia com o tempo $t$ numa posição fixa dada, por exemplo em $x = 0$ .
Se você se colocasse na posição $x = 0$ e observasse o movimento de um único “ponta” da corda, verificaria que o movimento é para cima e para baixo na diração $y$ seria dado segundo a equação

$y(0,t) = Asen( \pm \omega t)$

Onde foi tomado $x = 0$ na equação acima. Como $sen(- \alpha) = -sen(\alpha)$ esta última equação pode ser escrita como:

$y(t) = \pm Asen(\omega t)$

Onde simplificamos a notação de $y(0,t)$ para $y(t)$ apenas.
Um típico intervalo de período da onda é mostrado no item “a” da figura acima, onde o período da onda é $T = t_2 - t_1$ . Podemos notar que nos pontos $t_1 e t_2$ a função $y(t)$ possui o mesmo valor, ou seja:

$y(t_1) = y(t_2)$

Utilizando a equação $y(t) = \pm Asen(\omega t)$ podemos reescrever esta última equação como

$\pm Asen(\omega t_1)= \pm Asen(\omega t_2)$

Simplificando a constante A que aparece nos dois lados da igualdade:

$sen(\omega t_1) = sen(\omega t_2)$

Como $T = t_2 - t_1$ , podemos escrever que $t_2 = T + t_1$ e a equação anterior fica

$sen(\omega t_1) = sen(\omega t_1 + \omega T)$

Como já dissemos anteriormente a função seno se repete primeiramente quando o ângulo é acrescido de $2\pi$ radianos, de forma que a equação acima será verdadeira se $\omega T = 2\pi$ , ou

$\omega = \frac {2\pi}{T}$

sendo $\omega$ conhecido como frequência angular da onda, o que dá significado físico à quantidade $\omega$ que aparece na equação $y(x,t) = Asen (kx \pm \omega t)$ . A unidade de frequência angular no SI é o radiano por segundo (rad/s). Lembrando que o período da onda pode ser escrito em termos da frequência da onda como $T = 1/F$ , a equação $\omega = \frac {2\pi}{T}$ pode ainda ser escrita como

$\omega = 2\pi f$

Velocidade das Ondas Progressivas

Entendemos por ondas progressivas aquelas que se deslocam (para a esquerda ou direita) com o decorrer do tempo. Na figura 3.8 mostramos a onda da Eq. (3.7) em dois instantes $t_1$ e $t_2$ ou seja, em um intervalo de tempo $\deltat = t_2 - t_1$ . A onda está caminhando em direção crescente de $x$ ( para a direita Fig. 3.8) com uma configuração completa da onda deslocando-se de uma distância $\deltax$ durante o intervalo $\deltat$ . Fica claro que $\deltax = x_2 - x_1$ . A razão $\deltax/\deltat$ é a velocidade da onda. Como podemos encontrar em seu valor?

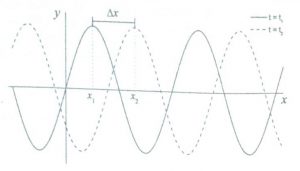
Figura 3.8: Onda deslocando na direção crescente de $x$ .

Utilizando a Eq. (3.4), que é a expressão do deslocamento longitudinal de uma onda que se desloca para a direita (sentido crescente de $x$ ).
Tomando a Eq. (3.4) para o instante $t = t_1$ e $t = t_2$ obtemos duas equações:

$x_1 = \frac {\alpha}{k} + \frac {\omegat_1}{k} ,$

(3.16)

$x_1 = \frac {\alpha}{k} + \frac {\omegat_2}{k} ,$

(3.17)

Respectivamente. Façamos agora a diferença entre estas duas equações, (3.17) – (3.16):

$x_2 - x_1 = \frac {\alpha}{k} + \frac {\omegat_2}{k} - \frac {\alpha}{k} - \frac {\omegat_1}{k}$

Simplificando e colocando $w/k$ em evidência temos

$x_2 - x_1 = \frac {\omega}{k}(t_2 - t_1) \centerdot$

Lembrando que $\deltax = x_2 - x_1$ e que $\deltat = t_2 - t_1$ esta última equação pode ser reescrita como

(

$\deltax = \frac {\omega}{k} \deltat ou \frac {\deltax}{\deltat} = \frac {\omega}{k} ,$

Sendo a velocidade definida como $v = \deltax / \deltat$ , temos finalmente

$v = \frac {\omega}{k} \centerdot$

(3.18)

A Eq. (3.18) nos dá então a velocidade com que a onda se propaga. Esta quantidade é positiva, indicando que a onda está viajando na direção crescente de $x$ , isto é, para a direita na Fig. 3.8. Se na dedução da equação para a velocidade da onda tivéssemos utilizado a Eq. (3.5) =, que é expressão do deslocamento longitudinal de uma onda que se desloca para a esquerda (sentido decrescente de $x$ ) teríamos obtido o seguinte resultado:

$v = - \frac {\omega}{k} ,$

(3.19)

Onde o sinal menos indica que a onda está viajando na direção decrescente de $x$ , isto é, para a esquerda. O leitor pode deduzir a Eq. (3.19) seguindo o mesmo processo utilizado para determinar a Eq. (3.18).
A Eq. (3.18) pode ser expressa de uma maneira alternativa. Fazendo uso da Eq. (3.11) ( $k = 2\pi/\lambda$ ) da Eq. (3.14) ( $\omega = 2\pi/T$ , podemos escrever, para a velocidade da onda.

$v = \frac {2\pi/T}{2\pi/\lambda}$

Que depois de simplificada se torna

$v = \frac {\lambda}{T} ,$

(3.20)

Como $f = 1/T$ , outra forma alternativa seria:

$v = \lambda f \centerdot$

(3.21)

A Eq. (3.20) nos diz que a onde se desloca de um comprimento de onda em um período de oscilação.
Um caso particular é uma onda se deslocando em uma corda. Pode ser demonstrado que a velocidade de propagação de uma onda numa corda ideal esticada, como a da Fig. 3.2, depende somente das características da corda e não da frequência da onda. Esta velocidade é expressa pela seguinte equação:

$v = \frac {r}{u} ,$

(3.22)

Onde $r$ é a tensão (ou tração) na corda e é a densidade linear de massada corda sendo definida como $u$ é a densidade linear de massa da corda, sendo definida como

$u = \frac {m}{L} ,$

(3.23)

Onde m e L são, respectivamente, a massa e o comprimento da corda. A unidade de (equação) no sistema internacional é kg/m. Percebemos da Eq. (3.22) que a velocidade de uma onda numa corda é caracterizada por dois aspectos: um elástico e outro inercial. A parte elástica da corda é representada pela tensão T na corda, pois não seria possível gerar uma onda numa corda esticada se esta corda não pudesse se esticar ainda mais.
A parte inercial da corda é representada pela sua densidade linear (equação), já que esta é a sua massa por comprimento. Ressaltamos aqui que todo meio em que se propagar uma onda mecânica existirá um aspecto elástico e outro inercial. A frequência da onda na corda esticada é fixada pelo agente que cria a onda (por exemplo, a mão da pessoa na Fig . 3.2). Poderemos determinar o comprimento de onda da onda na corda através da equação (equação).

Fenômenos Ondulatórios

Príncipio de Superposição

Pode ocorrer que duas ou mais ondas passem numa mesma região do espaço ao mesmo temPO. Seja, por exemplo, duas ondas 1 e 2 se deslocando simultaneamente ao longo de uma mesma corda esticada. O deslocamento da corda quando ambas as cordas atuam será.

(3.24)

Onde (equação) são os dois deslocamentos que a corda experimentaria se cada onda agisse separadamente. Esse é um exemplo do princípio de superposição, um princípio largamente utilizado na física, que se observa com bastante frequência Acústica. As Figuras 3.9 e 3.10 mostram dois pulsos, gerados nas extremidades de uma corda, em três instantes (equação)

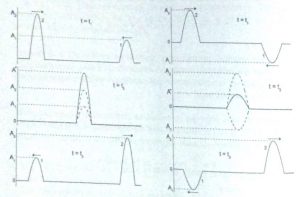
Figura 3.9: Interferência construtiva / Figura 3.10: Interferência destrutiva

Os dois pulsos se propagam em sentidos opostos. No instante (equação) os pulsos são produzidos. No instante (equação) eles se encontram e se superpõem, sendo que neste instante podemos aplicar o princípio de superposição (Eq. 3.24). No instante (equação), após os dois pulsos terem se encontrado, cada pulso continua se propagando em seu sentido original com a mesma velocidade, mesma amplitude e mesma frequência. É como se nada tivesse acontecido. No posto onde as duas ondas se encontraram ( no mesmo tempo e espaço) dizemos que ouve uma interferência. O fenômeno de interferência acontece com todos os tipos de ondas. O fenômeno é exclusivo do movimento ondulatório.

Interferência de Ondas

Interferência é o fenômeno de cancelamento ou de reforço quando uma ou mais ondas se superpõem. Seja, por exemplo, duas ondas que caminham ao longo de uma mesma corda esticada com a mesma frequência angular w e o mesmo número de onda angular k, definidas por

(3.25)

(3.26)

Onde (equação) são as amplitudes das ondas (equação), respectivamente. Estas duas ondas caminham no mesmo sentido (x crescente) com a sua velocidade sendo dada pela expressão (equação). As ondas (equação) e (equação) diferem apenas por uma constante (equação), a qual é chamada de diferença de fase, que representa a diferença de fase entre as duas ondas.
Aplicando o Princípio da Superposição, a onda resultante (equação), da combinação destas duas será

(equação)

Por questão de simplicidade trataremos apenas do caso em que as amplitudes das duas ondas sejam iguais, ou seja, (equação). Fazendo-se isto na questão anterior e definindo (equação), temos

(equação)

Utilizando a relação trigonométrica: (equação)

(equação)

Lembrando que (equação), temos finalmente

(3.27)

Notamos pela equação (3.27) que a onda resultante também possui uma forma senoidal, diferindo das ondas originais (equação), somente em dois aspectos: i) pela diferença de fase (equação) pela amplitude, que será

(3.28)

Dizemos, em geral, que se a onda resultante possui uma amplitude maior que as amplitudes das ondas originais, a interferência é construtiva ( Veja Fig. 3.9), e se a onda resultante possui uma amplitude menor que as amplitudes das ondas originais, a interferência é destrutiva ( Veja Fig. 3.10).
Verificamos agora dois casos bem especiais:
Primeiro caso: se fizermos (equação), na Eq. (3.27), ela se reduz a

(3.29)

Segundo caso: Verificamos que se (equação) na Eq. (3.27), (equação) e a onda resultante será nula:

(3.30)
No primeiro caso [Eq. (3.29)], as duas ondas (equação) e (equação) estão exatamente em fase e sua interferência é dita completamente construtiva.
Notamos pela Eq. (3.28) que para (equação) , a onda resultante possui uma amplitude que é o dobro da amplitude das ondas originais, ou seja, A* = 2A, sendo este o maior valor possível para a amplitude da onda resultante.
No segundo caso dizemos que houve uma interferência totalmente destrutiva e a amplitude da onda resultante possui seu valor mínimo, ou seja, (equação) na Eq. (3.28). Para que isto ocorra, as ondas originais devem estar exatamente em oposição da fase.

Passagem de uma Onda de um Meio para Outro

Na Fig. 3.11 (a) mostramos uma corda esticada, constituída de uma parte mais fina ligada a outra parte mais grossa. Temos então dois meios diferentes, (1) e (2), sendo particularmente, a densidade linear do meio (1) menor que a do meio (2), ou seja, (equação) Como tensão (equação) nas duas cordas é a mesma, podemos afirmar de acordo com a equação (3.22), que a velocidade de propagação de uma onda na parte mais fina é maior que na parte mais grossa, ou seja, (equação)
Fazendo oscilar a extremidade da corda fina, uma onda se propaga ao longo dela e, ao atingir a corda grossa passa a se propagar também nesta corda, isto é, a onda é transmitida da corda fina para a corda grossa (Fig. 3.11 (b)). A onda que é transmitida para o meio (2) recebe o nome de onda refratada.

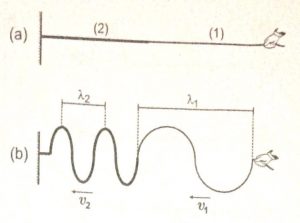
Figura 3.11: Refração de uma onda

A frequência de uma onda não se altera quando ela é transmitida de um meio para o outro, sendo o valor de f o mesmo para os meios (1) e (2). Pela equação (equação), vemos que, no meio em que a onda se propaga com maior velocidade, ela terá maior comprimento de onda e no meio em que a onda se propaga com menor velocidade ela terá um menor comprimento de onda. Assim, observe que na Fig. 3.11(b) temos (equação)
Concluindo, chamamos de refração de uma onda quando uma onda passa de um meio para outro, com variação da sua velocidade de propagação e de seu comprimento de onda. Na Figura 3.11 distinguimos então onda incidente (onda no meio 1) e a onda refratada (onda no meio 2). A onda refratada mantém a mesma frequência da onda incidente.

Reflexão de uma Onda

A reflexão de uma onda ocorre quando uma onda incide sobre um obstáculo e retorna ao meio original de propagação. A onda refletida mantém a mesma velocidade e o mesmo comprimento de onda da onda incidente.
Na Figura 3.12(a) mostramos a reflexão sofrida por um pulso quando incide em uma extremidade fixa. São mostrados quatro intervalos consecutivos de tempo (equação). Entretanto por extremidade fixa aquela que não pode se mover. O pulso é criado por uma pessoa na extremidade direita da corda e se propaga para a esquerda. Quando o pulso chega à extremidade esquerda encontra-se com uma parede onde a corda está fixada. O pulso exerce então uma força para cima sobre a parede. Pela lei de ação e reação (3° lei de Newton), a parede exercerá sobre a corda uma força de mesmo módulo mas de sentido contrário. Esta força de reação faz com que o pulso volte invertido em relação ao pulso incidente.

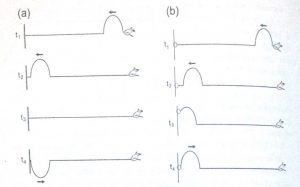
Figura 3.12: (a) Reflexão rígida e (b) reflexão não rígida.

Chamamos este tipo de reflexão de reflexão rígida. Deve-se notar que o ponto onde a corda está fixada na parede não sofre um deslocamento transversal. Chamamos este ponto de nó.
Na Figura 3.12 (b) mostramos a reflexão sofrida por um pulso quando incide em uma extremidade livre. Uma extremidade é dita livre quando ela pode se locomover. Para isto, na extremidade esquerda da corda foi colocado um anel que pode se deslocar por uma haste. Neste caso quando o pulso chega na extremidade esquerda da corda o anel desliza para cima na haste puxando a corda, produzindo um pulso refletido de mesmo sinal que o pulso incidente. Este tipo de reflexão é denominado de reflexão não rígida.
Além da refração e da reflexão existe um outro comportamento que a onda pode sofrer ao incidir sobre uma barreira: a ,em>difração. A difração de uma onda ocorre quando uma onda consegue “contornar” um obstáculo.