Número de onda e frequência angular

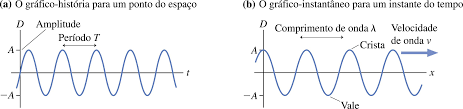
Na figura abaixo, mostramos como o deslocamento transversal $y(x,t)$ da equação $y(x,t) = Asen(kx \pm\omega t)$ varia em relação à posição $x$ num tempo determinado, escolhido com $t=0$ , isto é, a figura é um “instantâneo” da onda naquele momento. Com esta restrição, a equação acima torna-se

$y(x,0) = Asen(kx)$

Que por simplicidade escrevemos como

$y(x) = Asen(kx)$

Para um típico intervalo de comprimento de onda $\lambda = x_2 - x_1$ , podemos escrever a igualdade

$Asen(kx_1) = Asen(kx_2)$

Simplificando a constante A que aparece nos dois lados da igualdade:

$sen(kx_1) = sen(kx_2)$

Como $\lambda = x_2 - x_1$ , podemos escrever que $x_2 = \lambda + x_1$ e a equação anterior fica

$sen(kx_1) = sen(kx_1 + k \lambda)$

A função seno se repete primeiramente quando o ângulo é acrescido de $2\pi$ radianos, de forma que a equação acima será verdadeira se $k\lambda = 2\pi$ ou

$k = \frac{2\pi}{\lambda}$

Sendo $k$ conhecido como número de onda angular da onda. A relação apresentada na equação da sentido físico à quantidade $k$ que aparece na equação $y(x,t) = Asen(kx \pm \omega t)$ . A unidade de $k$ no SI é radiano por metro (rad/m).
Passamos agora nossa análise para o gráfico que mostra como o deslocamento $y$ da equação acima varia com o tempo $t$ numa posição fixa dada, por exemplo em $x = 0$ .
Se você se colocasse na posição $x = 0$ e observasse o movimento de um único “ponta” da corda, verificaria que o movimento é para cima e para baixo na diração $y$ seria dado segundo a equação

$y(0,t) = Asen( \pm \omega t)$

Onde foi tomado $x = 0$ na equação acima. Como $sen(- \alpha) = -sen(\alpha)$ esta última equação pode ser escrita como:

$y(t) = \pm Asen(\omega t)$

Onde simplificamos a notação de $y(0,t)$ para $y(t)$ apenas.
Um típico intervalo de período da onda é mostrado no item “a” da figura acima, onde o período da onda é $T = t_2 - t_1$ . Podemos notar que nos pontos $t_1 e t_2$ a função $y(t)$ possui o mesmo valor, ou seja:

$y(t_1) = y(t_2)$

Utilizando a equação $y(t) = \pm Asen(\omega t)$ podemos reescrever esta última equação como

$\pm Asen(\omega t_1)= \pm Asen(\omega t_2)$

Simplificando a constante A que aparece nos dois lados da igualdade:

$sen(\omega t_1) = sen(\omega t_2)$

Como $T = t_2 - t_1$ , podemos escrever que $t_2 = T + t_1$ e a equação anterior fica

$sen(\omega t_1) = sen(\omega t_1 + \omega T)$

Como já dissemos anteriormente a função seno se repete primeiramente quando o ângulo é acrescido de $2\pi$ radianos, de forma que a equação acima será verdadeira se $\omega T = 2\pi$ , ou

$\omega = \frac {2\pi}{T}$

sendo $\omega$ conhecido como frequência angular da onda, o que dá significado físico à quantidade $\omega$ que aparece na equação $y(x,t) = Asen (kx \pm \omega t)$ . A unidade de frequência angular no SI é o radiano por segundo (rad/s). Lembrando que o período da onda pode ser escrito em termos da frequência da onda como $T = 1/F$ , a equação $\omega = \frac {2\pi}{T}$ pode ainda ser escrita como

$\omega = 2\pi f$