Ondas Sonoras

Ondas Sonoras

As ondas sonoras são ondas longitudinais de compressão/rarefaçao que se propagam num meio material – sólido, líquido ou gasoso, e que são susceptíveis de provocar uma sensação auditiva. Como já foi referido, as ondas dizem-se longitudinais porque as moléculas oscilam para frente e para trás, no mesmo sentido de propagação das ondas. As ondas sonoras que se propagam num gás, no ar por exemplo, podem ser consideradas como ondas de densidade ou de pressão. Na secção B.15 é referido que densidade e pressão são grandezas adequadas ao estudo dos fluidos, por variarem de ponto para ponto. As ondas sonoras originam perturbações da densidade do meio, provocadas pelas mudanças na pressão, velocidade das partículas e temperatura no fluido em que se propagam.
Ondas e sons são fenómenos de natureza diferente: os sons são fenómenos, temporais enquanto que as ondas são fenómenos simultaneamente temporais e espaciais. Logo, descrição matemática de uma onda denominada equação de onda, envolve as grandezas tempo e espaço. Os fenómenos de propagação e de radiação das ondas sonoras são descritos por essas equações, as quais serão expostas na secção 4.5.
Das grandezas que caracterizam uma onda sonora, a mais facilmente mensurável é a pressão usando um transdutor sensível a flutuação de pressão, como é o caso de um microfone. A velocidade das partículas pode também ser medida indirectamente utilizando uma sonda de intensidade (Veja secção 5.19).

Dimensão do Meio de Propagação

O meio de propagação das ondas sonoras pode ser sólido, líquido ou gasoso. Relativamente à dimensão do meio, ele pode ser, unidimensional, bidimensional ou tridimensional. Seja qual for a dimensão do meio considerado, há propriedades comuns particularmente material, ou massa volúmica, é a massa de uma unidade de volume. Consoante a dimensão do meio, assim a densidade se expressa em unidades convenientes: a massa de uma unidade de comprimento, a massa de uma unidade de superfície ou a massa de uma unidade de volume, respectivamente para o meio uni, bi e tridimensional (Veja Tabela 4.1).

Tabela 4.1 Dimensão do meio de propagação
Velocidade de Propagação

A propagação do som faz-se através do movimento das partículas do meio. Essas partículas têm massa e elasticidade, logo, o meio pode ser idealizado como uma quantidade muito grande de osciladores. Vejamos o que se estende por partícula de fluído.
A distância percorrida pelas moléculas de ar entre as duas colisões – percurso livre médio (mean free path) -, é muito pequena (equação) (veja secção 19.13). Podemos considerar pequenos volumes de ar muito menores do que o comprimento de onda mas muito maiores do que o percurso livre médio. Esses volumes têm uma quantidade de moléculas bem definidas. A massa desses pequenos volumes não varia significativamente com os movimentos individuais das moléculas e tem uma densidade bem definida. Um tal volume é designado partícula do fluido (Prandtl & Tietjens, 1934).
6 *No apêndice B são incluídas várias considerações sobre as propriedades dos materiais, com o objetivo de uma melhor compreensão da propagação do som nos diversos meios. Aconselha-se a leitura prévia deste apêndice.

Sincronização de Grandes Massas Orquestrais e Corais

A velocidade de propagação da luz é de 300 000 km s –1, enquanto que o da propagação do som é da ordem de 0.344 km s-1. Desta diferença substancial de valores, resulta um fenómeno bem conhecido: quando ouvimos um estrondo ao longe (foguete, trovão), vemos a luz que lhe está associada, e só mais tarde chega até nós o som desse acontecimento. Nos estádios esportivos, os espectadores divertem-se explorando esse defasamento: cantando e levantando-se simultaneamente, dos dois lados do estádio, ou fazenda a “onda”. Devido à distância considerável entre as bancadas, o som chega um pouco mais tarde.
Esse fenómeno tem implicações em música. Para pequenas distâncias de propagação, praticamente não existe defasamento entre a observação dos fenómenos e o som por eles emitido. No entanto, para distância de vinte metro ou superiores, apercebemo-nos de que o som leva algum tempo a chegar. Em concertos ou óperas realizados em grandes salas, o fenómeno é bem perceptível para o público que se encontra nos lugares mais distantes do palco. Os movimentos dos músicos e cordas nas arcadas surgem antes da chegada do som que emitem. Os movimentos do maestro também são reveladores desse defasamento temporal.
Mas, se para o público é apenas um pequeno contratempo sem consequência na audição musical, para os músicos a realidade é diferente. Se o palco é pequeno e o número de músicos reduzido, o problema não se põe. No entanto, em obras sinfónicas e coral – sinfónicas, óperas, em que podem estar duzentas ou trezentas pessoas num palco muito grande (sem pensar em obras gigantescas, como a sinfonia nº 8 dos mil), a acção coordenadora do maestro é essencial para a sincronização dos músicos mais distantes

.

(tabela)

Consideremos um determinado meio de propagação. Quando se provoca uma perturbação nesse meio, a onda originada leva um certo tempo a atingir outros pontos no meio que estamos a considerar. A velocidade de propagação do som (por vezes também designada velocidade da onda) depende das características desse meio, nomeadamente a elasticidade e a densidade, as quais dependem da temperatura. Em geral, a velocidade de propagação de uma onda mecânica através de um meio, é uma expressão da forma (Benade, 1990; Benson, 1996):

(equação)

A análise dos valores na Tabela 4.2 mostra que, saldo algumas excepções (chumbo, por exemplo, a velocidade de propagação do som é maior nos sólidos a seguir nos líquidos e finalmente nos gases, o que está de acordo com as características mecânicas e a estrutura dos estudos da matéria.
Relativamente ao ar, verifica-se que a dissipação termo – viscosa de energia depende muito da humidade e da poluição.

Qualidades Fisiológicas do Som

Nosso aparelho auditivo distingue no som certas características, denominadas qualidades fisiológicas, que são altura, intensidade e timbre.

Altura

A qualidade pela qual diferenciamos sons graves de sons agudos é denominada altura. Ela depende apenas da frequência do som.
O som será tanto mais grave quanto menor for a sua frequência. Ela será tanto mais agudo quanto maior for sua frequência. Por exemplo, o homem costuma emitir sons entre 100 e 200 Hz,e a mulher sons entre 200 e 400 Hz. Dizemos então que a voz do homem é mais grave que a da mulher ou que a voz da mulher é mais aguda que a do homem.

Denomina-se intervalo entre dois sons de frequência f, e f, sendo(equação)
Quando (equação), os sons estão em uníssono; quando (equação), o intervalo é denominado oitava.
Em música (Veja a leitura abaixo: A escala musical) utilizam-se outros intervalos, geralmente chamados intervalos musicais. Por exemplo, o intervalo (equação) é denominado tom maior (equação) é o tom menor (equação) é o semitom etc.

A escala musical

A denominada escala musical natural ou diatônica é formada por sons (notas musicais) que guardam entre si intervalos bem-definidos na sequência: tom maior, tom menor, semitom, tom menor, tom maior, semitom.
Por exemplo, considerando a escala natural de dó maior, teríamos:

A notação musical que usamos (bolinhas sobre o pentagrama) foi criação do monge beneditino Guido de Arezzo, no século XI, que também “batizou” as notas a partir de um hino sacro em homenagem a São João:

Com o tempo, “ut foi substituído por “dó”.

Intensidade

A qualidade fisiológica pela qual diferenciamos os sons fracos dos sons fortes é denominada intensidade auditiva e sonoridade, ou ainda nível sonoro do som. Depende da energia transportada pela onda sonorae, portanto, de sua intensidade física.
A intensidade física*/de uma onda, como já definimos anteriormente, é o quociente entre a energia (equação) que atravessa uma superfície (perpendicular à direção de propagação) na unidade de tempoe a área A da superfície (figura 4).

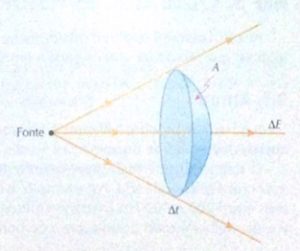
Figura 4. A intensidade de uma onda é a medida da energia que atravessa uma superfície pela área na unidade de tempo.

*Para evitar confusão, aqui vamos chamar a intensidade da onda de intensidade física.
O quociente (equação) constitui a potência Pot da onda, isto é, (equação). Nessas condições, temos:

(equação)

No sistema internacional de Unidades, sendo (equação) medido em joules, A em m² em segundos, a unidade de intensidade física é o j/m² . Ou W/m².
A mínima intensidade física que uma onda sonora deve ter para ser audível (limiar de audição) é aproximadamente (equação). Por outro lado, se a intensidade exceder aproximadamente 1 W/m², ela provocará efeitos dolorosos (limiar da dor).
O sistema auditivo humano não é excitado linearmente pela intensidade física do som. Assim, ao se dobrar a intensidade física de um determinado som, distingue-se um som mais forte, porém não duas vezes mais intenso.
Experiências mostram que, para medir a intensidade auditiva, também denominada nível sonoro do som, deve-se utilizar uma escala logarítmica.
Considerando(equação) a menor intensidade física de som audível (geralmente adota-se (equação)intensidade física do som que se quer medir, define-se intensidade auditiva ou nível sonoro (equação) de um som como o expoente a que se deve elevar o número 10 para se obter a relação (equação) então:

Nessa fórmula, (equação) é medida em bel (simbolo B), nome dado em homenagem a Alexandre Graham Bell*, inventor do telefone.
Na prática geralmente medimos (equação) em uma unidade menor, o decibel (cB), sendo (equação)

(equação)

O som do tráfego na cidade é de 90 dB; um conjunto de rock, usando amplificador, produz intensidade audíveis de 125 dB, e o som de um avião a jato aterrissando é de aproximadamente 140 dB. Já está provado que uma exposição prolongada a níveis sonoros acima de 85 dB geralmente ocasiona uma dano permanente às estrutura auditivas do ouvinte.

A avaliação do nível sonoro de um ambiente é feita com aparelhos denominados decidelímetros.

*BELL, Alexandre Graham, (1847-1922), cientista escocês naturalizado norte-americano, fez inúmeros estudos no campo da Acústica. Sua grande contribuição para o desenvolvimento tecnológico de nossa civilização foi a invenção do microfone e, sobretudo, a do telefone.

Timbre

Quando um instrumento musical emite determinada nota, diversos sons de frequências múltiplas se superpõem para constituir essa nota. Desse sons, o de menor frequência constitui o som fundamental, e os demais, com frequências múltiplas, são os harmônicos. Assim, sendo (equação) a frequência do som fundamental, podemos ter o segundo harmônico (equação), o terceiro harmônico (equação) e assim sucessivamente. A superposição do som fundamental com os harmônicos determina a forma da onda emitida pelo instrumento, como se representa na figura 5.

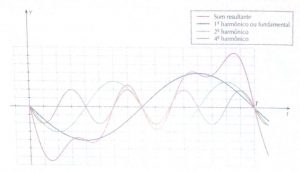
Figura 5. Composição dos sons emitidos por um instrumento.

O som fundamental ou primeiro harmônico está sempre presente e é ele que determina a frequência do som emitido. Os harmônicos que acompanham o som fundamental variam de instrumento para instrumento. É essa característica que torna distintos, para o ouvinte, sons da mesma altura (mesma frequência) emitidos por instrumentos diferentes, mesmo que esses sons tenham a mesma intensidade. A essa qualidade fisiológica do som damos o nome de timbre.

Propriedade das ondas sonoras<

As ondas sonoras apresentam as mesmas propriedades dos demais tipos de ondas: reflexão, refração, difração e interferência.
Elas só não podem ser polarizadas porque não são ondas transversais.

Reflexão sonora, Reforço, reverberação e eco

A reflexão do som pode dar origem ao reforço, à reverberação ou ao eco, dependendo do intervalo de tempo entre a percepção, pelo ouvinte, do som direto e do som refletido.

A ocorrência de um ou de outro desses fenômenos deve-se ao fato de só conseguirmos distinguir dois sons que nos chegam com um intervalo de tempo superior a 0,1 s (um décimo de segundo). Esse intervalo de tempo é denominado persistência auditiva.
Se o obstáculo que reflete o som estiver muito próximo, o som direto e o som refletido chegam praticamente no mesmo instante. O ouvinte terá então a sensação de um som mais forte. A esse fenômeno se dá o nome de reforço.
Quando o obstáculo refletor está mais afastado, de modo que o intervalo entre a percepção do som direto e a do som refletido é menor que 0,1 s, mas não é desprezível, ocorre o fenômeno da reverberação. Nesse caso o som refletido chega ao sistema auditivo, enquanto a sensação do som direto ainda não se extinguiu. O ouvinte tem então a impressão de um prolongamento do som. Nos auditórios, a reverberação, desde que não exagerada, auxilia o entendimento do que está sendo falado.
O eco ocorre, quando o som refletido é recebido pelo ouvinte depois que o som direto já se extinguiu. Assim, o ouvinte percebe dois sons distintos. Para que isso aconteça, o intervalo de tempo entre percepção dos dois sons (direto e refletido) deve ser maior que 0,1 s. Considere a situação da figura 6: uma pessoa situada a uma distância x de uma parede grita um monossílabo. Para haver eco devemos ter: (equação).

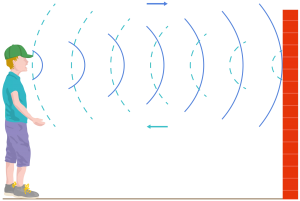
Figura 6. Para haver eco, deve-se ter x>17m.

Mas, de (equação)
A condição para que ocorra o eco é: (equação). Sendo v = 340 m/s a velocidade do som no ar e (equação) (ida e volta), vem:

(equação)

Portando, um ouvinte percebe que o eco desde que sua distância ao obstáculo refletor seja superior a 17 m no ar.

O Sonar

O sonar (Sound Navigation And Ranging) é um dispositivo que, instalado em navios e submarinos, possibilita medir profundades oceânicas e detectar a presença de obstáculos. Originalmente foi desenvolvido com finalidades bélicas, durante a Segunda Guerra Mundial (1939-1945), como um meio de localizar submarinos e outras embarcações do inimigo.
Seu funcionamento baseia-se na reflexão de ondas sonoras. O sonar emite ultra-sons e capta as ondas que se refletem no eventual obstáculo, medindo o intervalo de tempo entre a emissão e a recepção. Conhecida a velocidade de propagação das ondas sonoras na água, é possível determinar a que distância se encontra o obstáculo refletor.

Emitido ultra-sons e recebendo as ondas refletidas os morcegos localizam alimentos, como flores, frutos e insetos, e evitam colisões com obstáculos enquanto voam, mesmo em plena escuridão.

Esquema do sonar.

Refração e difração sonora

A refração do som ocorre quando uma onda produzida em um meio passa para outro meio em que sua velocidade é diferente. Nesse caso, a frequência do som permanece a mesma, modificando-se seu comprimento de onda.
A difração do som possibilita que as ondas sonoras contornem obstáculos com dimensões de até 20 m. Considerando que a velocidade do som no ar, em determinadas condições, é v = 340 m/s, e que o sistema auditivo humano distingue sons de frequência (equação)

(equação)

Na prática considera-se essa variação entre 2 cm e 20 m. Assim, a difração das ondas audíveis no ar é bem perceptível quando os obstáculos a serem contornados tem dimensões dessa ordem de grandeza.

Interferência sonora

A interferência do som pode ocorrer quando um ponto do meio recebe dois ou mais sons originados por várias fontes ou reflexões em obstáculos.

Valem, para a interferência das ondas sonoras, as mesmas condições estabelecidas para as ondas em geral. Chamando de d a diferença entre as distâncias percorridas
Fontes em concordância de fase (ou em fase)

(equação)

Fontes em oposição de fase

(equação)

Um caso importante de interferência sonora é o denominado batimento, que ocorre quando há interferência de ondas sonoras de frequência ligeiramente diferentes. A intensidade varia de um som forte, que se ouve em dado instante, para um silêncio quase total; a seguir novamente o som forte, e assim por diante. A razão desse comportamento é mostrada na figura 7: os sons fortes ocorrem quando as ondas interferem construtivamente, reforçando-se umas às outras, e o silêncio, quando há interferência destrutiva e as ondas se anulam total ou parcialmente. A frequência do batimento (equação) é igual à diferença entre as frequências componentes:

(figura)

Figura 7. Batimentos

O ser humano distingue batimentos até uma frequência (equação)

É comum os músicos de uma orquestra afinarem seus instrumentos utilizando o fenômeno de batimentos. Enquanto as frequências (do instrumento e da fonte afinadora) são diferentes, mas próximas ouvem-se os batimentos. À medida que o instrumento vai sendo afinado, a frequência de batimento vai diminuindo até desaparecer quando as frequências se tornam iguais.

A tecnologia do silêncio

A eliminação de ruídos indesejáveis pode ser feita utilizando-se o fenômeno da interferência. Microfones captam os ruídos do ambiente e enviam a um computador. Este analisa o som recebido e emite outro, em oposição da fase relativamente ao som captado. Da superposição das duas ondas resulta uma interferência destrutiva e, consequentemente, o silêncio.
Seguindo essa mesma diretriz, algumas indústrias do setor automotivo têm instalado em veículos pesados, como caminhões de grande tonelagem, um silenciador eletrônico para motores a explosão. Esse dispositivo consiste em um microprocessador que produz ondas sonoras de mesma frequência que as emitidas pelo motor, mas em oposição de fase. Essas ondas se superpõem às originais e determinam uma interferência destrutiva, isto é, o silêncio, garantindo o conforto sonoro para os usuários de veículo e para a população em geral.

Cordas vibrantes. Ressonância

Considere a corda de massa m, comprimento L e, portanto, densidade linear (equação) da figura 8, fixada nas extremidades e submetida à força de tração T. Provocando-se ondas transversais nessa corda, por exemplo, mediante uma percussão, elas se propagam com velocidade.

(equação e imagem)

Figura 8. Ondas estacionárias em uma corda vibrante

A propagação dessas ondas e sua reflexão nas extremidades determinam a formação de ondas estacionárias, com nós nas extremidades. Essas ondas estacionárias provocam no ar regiões de compressão e rarefação, isto é, originam ondas sonoras.
Em vista da formação de nós nas extremidades fixas (figura 8), as ondas que se propagam na corda apresentam comprimento de onda iguais a:

(equação)

E assim por diante.
A condição de formação de nós em cada extremidade restringe, portanto, os possíveis comprimentos de ondas das ondas que originam as ondas estacionárias a:
(equação)
A menor frequência (equação) de vibração da corda corresponde ao comprimento de onda (equação) = 2L. Fazendo n = 1 na expressão anterior, temos:

(equação)

Frequências maiores correspondem a comprimentos de onda menores. De maneira geral.

(equação)

Essas frequências maiores podem ser indicadas em função da menor frequência (equação) por:

(equação)

A vibração que corresponde à frequência (equação) é chamada de fundamental ou primeiro harmônico, e vibrações de frequência (equação)…são os harmônicos da fundamental. Então (equação) é o segundo harmônico, (equação) é o terceiro harmônico, e assim por diante.
A frequência fundamental e os harmônicos de uma corda vibrante são suas frequências naturais de vibração. É importante observar que, se a corda for percutida arbitrariamente, uma ou mais dessas frequências poderão ser estimuladas. Os harmônicos se superpõem, determinando a forma da onda e caracterizando o timbre do som emitido.
A resistência do meio onde a corda se encontra fará com que as vibrações desapareçam aos poucos. Pode-se fazer com que as vibrações persistam percutindo-se periodicamente a corda com frequência igual a uma de suas frequências naturais. A ondas estacionárias continuarão enquanto a percussão periódica fornecer energia à corda.
Qualquer fonte sonora produz no ar vibrações que estimulam oscilação em corpos situados nas proximidades. Quando a frequência da fonte coincide com uma frequência natural de oscilação do corpo, a amplitude de oscilação deste atinge valores elevados, pois a fonte progressivamente cede energia ao corpo. Esse fenômeno é denominado ressonância. Um exemplo de ressonância é a quebra de uma taça de cristal quando um violino, nas proximidades, é tocado com frequência igual a uma das frequências naturais de vibração da taça.
Outros exemplos de ressonância

Sempre que um sistema vibrante recebe energia periodicamente com frequência igual a uma de suas frequências naturais de vibração, esse sistema entra em ressonância em muitas situações, sem que ondas estejam envolvidas.
Empurrando-se periodicamente em balanço com frequência igual à do balanço, este oscila com amplitudes cada vez maiores.
A ponte do rio Tacoma, nos Estados Unidos ruiu em 1940, quando uma ventania lhe imprimiu impulsos periódicos com frequência igual a uma frequência natural de vibração da ponte.

Ao sintonizar uma emissora de rádio, fazemos com que o circuito do aparelho entre em ressonância com a frequência das ondas da emissora
(imagem)

A destruição da ponte do rio Tacoma (Washington Estados Unidos) é um bom exemplo de ressonância. Inaugurada em 1º de julho de 1940, foi destruída quatro meses após, por vibração provocada pelo vento.
Num violão, o ar da caixa de ressonância vibra com frequência igual à corda tocada, intensificando o som.
A concha acústica presente em muitos auditórios, por parte da platéia, dos sons emitidos. Seu funcionamento baseia-se no fenômeno da ressonância. As características geométricas da concha é que determinam as frequências sonoras que são intensificadas.
Se uma ampola contendo vapor de mercúrio for posta ao lado de um lâmpada de vapor de mercúrio acesa, a ampola passa a emitir luz em virtude da ressonância.

Colunas de ar vibrante. Tubos sonoros

Considere uma fonte sonora, por exemplo um diapasão, vibrando sobre a extremidade aberta de um tubo de vidro parcialmente preenchido com água.
Em certas condições, o som emitido pelo diapasão é reforçado, aumentando sua intensidade: quando o reservatório R da figura 9 é levantado, o nível da água no tubo sobe e verifica-se existirem determinadas posições do nível de água para as quais a coluna de ar no tubo vibrando entra em ressonância com o som emitido pelo diapasão.
As ondas sonoras emitidas pelo diapasão propagam-se pelo ar no tubo e interferem com as ondas refletidas na superfície da água, originando ondas estacionárias no ar.
O tubo da figura 9 terá um nó na extremidade fechada e um ventre na extremidade aberta, conforme ilustrado na figura 10. De fato, na extremidade fechada, as moléculas de ar do tubo são impedidas de se movimentarem pela superfície da água, enquanto, na extremidade aberta, elas se movimentam facilmente para o espaço aberto.
Então o ar no tubo somente entra em ressonância para ondas que se encaixam no comprimento L do tubo, com um nó na extremidade fechada e um ventre na aberta, como esquematizado na figura 10. Como a distância entre um nó e um ventre é igual a um quarto do comprimento de onda, têm-se os seguintes comprimentos de onda:

(equação)

E assim por diante.
A condição de formação de nó na extremidade fechada e de ventre na aberta restringe portanto os possíveis comprimentos de onda das ondas que originam as ondas estacionárias no tubo fechado a:

(equação)

Figura 9. Ressonância de uma coluna de ar com um diapasão.

Figura 10. Modos naturais de vibração de uma coluna de ar em um tubo fechado numa extremidade. As regiões mais escuras, onde a pressão do ar é maior correspondem ao nós.

Efeito Doppler

Considere um observador O parado na calçada de uma rua quando uma ambulância passa com a sirene ligada. O observador nota que a altura do som da sirene diminui repentinamente depois que a ambulância o ultrapassa. Uma observação mais detalhada revela que a altura sonora da sirene é maior quando a ambulância se aproxima do observador e menor quando a ambulância se afasta. Esse fenômeno, junto com outras situações físicas nas quais ele ocorre, é denominado efeito Doppler*.
Na figura 13, considere o observador O parado na calçada e a sirene (fonte sonora) aproximando-se dele com velocidade (equação). No instante t = 0 a fonte emitiu a frente de onda (equação). Seja v a velocidade de propagação do som. Considere que essa frente de onda atinge o observador no intervalo de tempo igual ao período T de emissão de ondas sonoras pela fonte. A frente de onda (equação) percorreu, nesse intervalo de tempo, a distância vT na direção e sentido do observador, enquanto a fonte percorreu a distância (equação) na mesma direção e sentido do observador, e está agora emitindo a frente de onda (equação). A distância entre as frentes de onda (equação) e (equação) será comprimento de onda (equação) das ondas sonoras recebidas pelo observador O.

(figura)

Figura 13. O observador parado recebe o som emitido pela ambulância com frequência aparente f’ maior que a frequência f real.
Temos (equação) e, para o observador as ondas sonoras terão frequência aparente:
Com a frequência real f do som emitido pela fonte vale (equação) , decorre:
(equação) v

Então a frequência aparente f’ do som, que atinge o observador partindo de uma fonte em movimento que se aproxima dele, é maior que a frequência real f do som.
Se a ambulância estiver se afastando do observador, seguindo o mesmo raciocínio anterior, concluímos que:
(equação)
Doppler*, Cristian Johan (1803-1853) , físico austríaco, descreveu o fenômeno que leva seu nome (efeito Doppler) para o som e para a luz. O efeito Doppler para a luz foi explicado corretamente pelo físico francês Amand Hyppolyte Louis Fizeau (1819-1896), em 1848. Fizeau foi o primeiro cientista a determinar experimentalmente a velocidade da luz, em 1849 é usado para a descoberta de estrelas duplas.
Nesse caso, a frequência aparente f’ do som ouvido de uma fonte que está se afastando do observador é menor que a frequência real f do som.
Observa-se também uma mudança na altura do som se a fonte está em repouso e o observador é que se movimenta. Neste caso, a frequência aparente do som é maior que a real quando o observador se aproxima, e menor quando ele se afasta.
De modo geral, podemos concluir a seguinte relação entre a frequência aparente f’ do som que atinge o observador e a frequência real f do som emitido pela fonte:
(equação)
Em que v é a velocidade do som (equação) é a velocidade da fonte e (equação) a velocidade do observador.
O sinal que precede (equação) é definido em relação a um eixo orientado do observador para fonte:
(equação)
Evidentemente, se o observador estiver parado (equação) = 0 e, se a fonte estiver parada (equação)

O efeito Doppler para a luz

As ondas luminosas também podem sofrer o efeito Doppler. Entretanto, como a velocidade da luz é muito elevada, ele só é perceptível se a fonte for extremamente veloz. É o caso de estrelas ou galáxias que se afastam da terra.
Quando a fonte está se afastando, a luz recebida por nós tem frequência aparente f’ menor que a frequência real f emitida. Dizemos, então, que houve um desvio para o vermelho (no espectro visível, a luz vermelha é a de menor frequência).
Caso a fonte esteja se aproximando, recebemos uma luz cuja frequência aparente f’ é maior que a frequência real emitida f, tendo havido então desvio para a violeta ( no espectro visível, a luz violeta é a de maior frequência).
Em resumo: