Velocidade das ondas progressivas
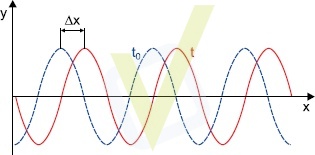
Entendemos por ondas progressivas aquelas que se deslocam (para a esquerda ou direita) com o decorrer do tempo. Na figura abaixo, mostramos uma onda em dois instantes ![]() e
e ![]() ou seja, em um intervalo de tempo
ou seja, em um intervalo de tempo ![]() . A onda está caminhando em direção crescente de
. A onda está caminhando em direção crescente de ![]() (para a direita da figura) com uma configuração completa da onda deslocando-se de uma distância
(para a direita da figura) com uma configuração completa da onda deslocando-se de uma distância ![]() durante o intervalo
durante o intervalo ![]() . Fica claro que
. Fica claro que ![]() . A razão
. A razão ![]() é a velocidade da onda.
é a velocidade da onda.
Utilizando a equação ![]() , que é a expressão do deslocamento longitudinal de uma onda que se desloca para a direita (sentido crescente de
, que é a expressão do deslocamento longitudinal de uma onda que se desloca para a direita (sentido crescente de ![]() ). Tomando essa equação para os instantes
). Tomando essa equação para os instantes ![]() e
e ![]() obtemos duas equações:
obtemos duas equações:
![]()
![]()
Respectivamente. Façamos agora a diferença entre estas duas equações:
![]()
Simplificando e colocando ![]() em evidência temos
em evidência temos
![]()
Lembrando que ![]() e que
e que ![]() , esta última equação pode ser reescrita como
, esta última equação pode ser reescrita como
![]()
ou
![]()
Sendo a velocidade definida como ![]() , temos finalmente
, temos finalmente
![]()
A equação acima nos dá então a velocidade com que a onda se propaga. Esta quantidade é positiva, indicando que a onda está viajando na direção crescente de ![]() , isto é, para a direita. Se na dedução da equação para a velocidade da onda tivéssemos utilizado a equação
, isto é, para a direita. Se na dedução da equação para a velocidade da onda tivéssemos utilizado a equação ![]() , que é a expressão do deslocamento longitudinal de uma onda que se desloca para a esquerda (sentido decrescente de
, que é a expressão do deslocamento longitudinal de uma onda que se desloca para a esquerda (sentido decrescente de ![]() ) teríamos obtido o seguinte resultado:
) teríamos obtido o seguinte resultado:
![]()
Onde o sinal menos indica que a onda está viajando na direção decrescente de ![]() , isto é, para a esquerda.
, isto é, para a esquerda.
A equação ![]() pode ser expressa de uma maneira alternativa. Fazendo uso da equação
pode ser expressa de uma maneira alternativa. Fazendo uso da equação ![]() e da equação
e da equação ![]() , podemos escrever, para a velocidade da onda.
, podemos escrever, para a velocidade da onda.
![]()
Que depois de simplificada se torna
![]()
Como ![]() , outra forma alternativa seria:
, outra forma alternativa seria:
![]()
Um caso particular é uma onda se deslocando em uma corda. Pode ser demonstrado que a velocidade de propagação de uma onda numa corda ideal esticada, depende somente das características da corda e não da frequência da onda. Esta velocidade é expressa pela seguinte equação:
![]()
Onde ![]() é a tensão (ou tração) na corda e
é a tensão (ou tração) na corda e ![]() é a densidade linear de massa da corda, sendo definida como
é a densidade linear de massa da corda, sendo definida como![]() é a densidade linear de massa da corda, sendo definida como
é a densidade linear de massa da corda, sendo definida como
![]()
Onde m e L são, respectivamente, a massa e o comprimento da corda. A unidade de ![]() no sistema internacional é kg/m. Percebemos da equação
no sistema internacional é kg/m. Percebemos da equação ![]() que a velocidade de uma onda numa corda é caracterizada por dois aspectos: um elástico e outro inercial. A parte elástica da corda é representada pela tensão
que a velocidade de uma onda numa corda é caracterizada por dois aspectos: um elástico e outro inercial. A parte elástica da corda é representada pela tensão ![]() na corda, pois não seria possível gerar uma onda numa corda esticada se esta corda não pudesse se esticar ainda mais.
na corda, pois não seria possível gerar uma onda numa corda esticada se esta corda não pudesse se esticar ainda mais.
A parte inercial da corda é representada pela sua densidade linear ![]() já que esta é a sua massa por comprimento. Ressaltamos aqui, que todo meio em que se propagar uma onda mecânica existirá um aspecto elástico e outro inercial. A frequência da onda na corda esticada é fixada pelo agente que cria a onda. Poderemos determinar o comprimento de onda da onda na corda através da equação
já que esta é a sua massa por comprimento. Ressaltamos aqui, que todo meio em que se propagar uma onda mecânica existirá um aspecto elástico e outro inercial. A frequência da onda na corda esticada é fixada pelo agente que cria a onda. Poderemos determinar o comprimento de onda da onda na corda através da equação ![]() .
.
